在这里先介绍一下章文嵩先生:曾是淘宝网高级研究员、核心系统负责人,主要负责基础核心软件研发、推进网络软硬件方面的性能优化、搭建下一代高可扩展低碳低成本的淘宝电子商务基础设施。他也是Linux内核的开发者,著名的Linux集群项目—LVS(Linux
Virtual Server)的创始人和主要开发人员,LVS集群代码已在Linux
2.4和2.6的官方内核中,并得到广泛的应用。在架构大型系统、系统软件开发、Linux操作系统、网络和软件开发管理上有着丰富的经验。他一直在自由软件的开发上花费时间,并积极推动开源活动在中国的发展。

2016年5月27日,任滴滴出行高级副总裁、负责CTO线基础平台部兼工程技术委员会主席。
加入滴滴之前,章文嵩曾在阿里巴巴任职近七年,历任淘宝网资深技术总监、淘宝技术委员会主席、阿里副总裁、阿里开源委员会主席、阿里云CTO等。
最近一段滴滴副总裁章文嵩演讲的视频在网络上传播,引起了争议,完整版视频如下:https://v.qq.com/x/page/x06289x4zmc.html
视频在微博引发争议性传播:


章文嵩指出标题有误,他微博回复称:朋友把这个微博转给我,这标题明显误导。我是表达派单问题的复杂度,搜索空间是巨大的,并没有对比滴滴算法和AlphaGo算法,实际上我们也使用增强学习算法。
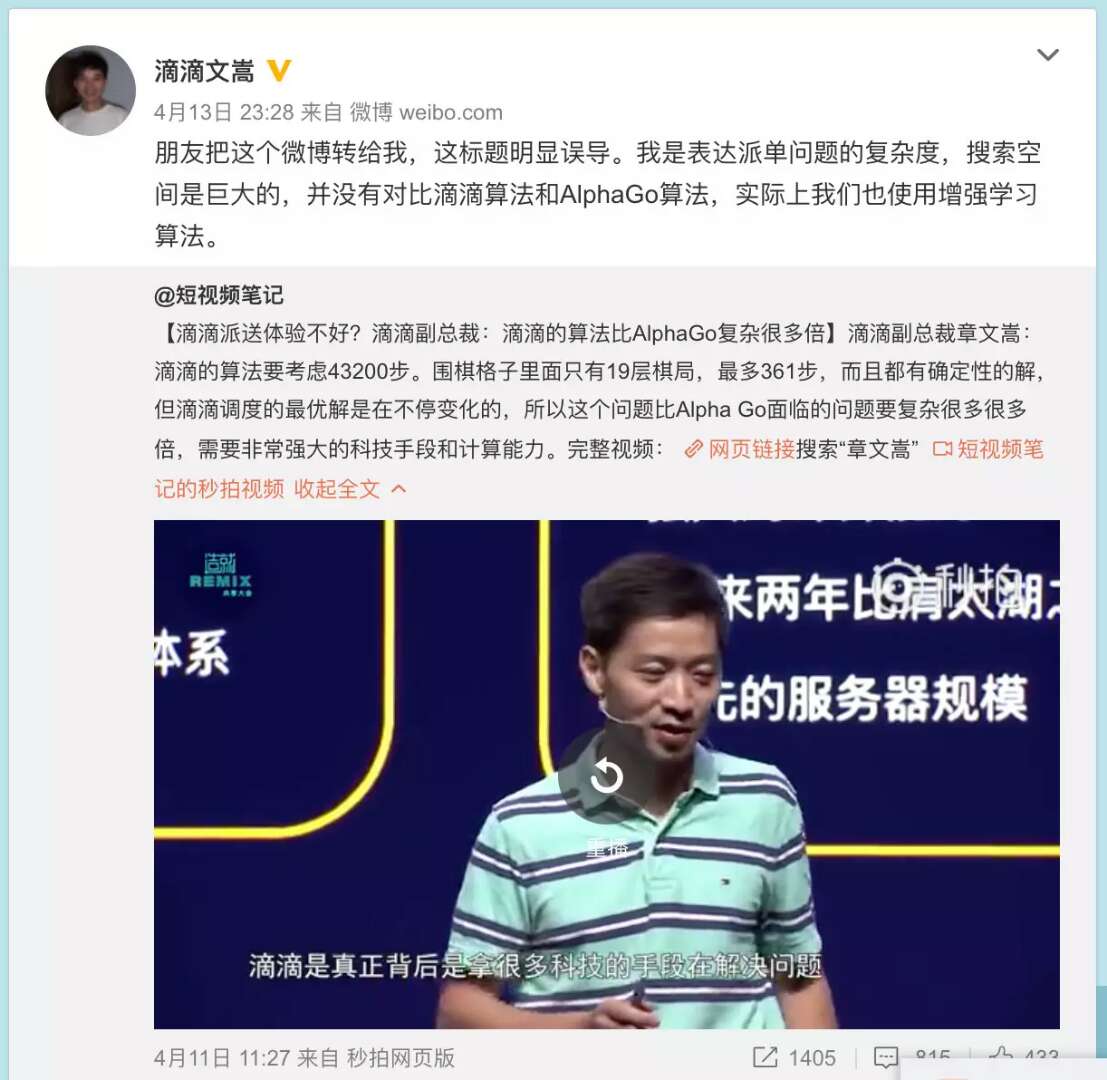
4月14日再次针对此事在微博进行评论:
章文嵩:昨天朋友发给我两位围棋届名人对滴滴派单问题的评论,可能他们并没有真正进来了解滴滴派单问题,也有可能我上次的演讲没有解释清楚,有必要进一步讨论一下。
在围棋里,每一步落子都会影响棋局变化。在19*19的棋盘上,最多对弈361步,若不考虑棋盘的对称性,围棋的变化是361的阶乘,约10的768次方...,这已经是一个惊人的量。
滴滴派单问题是极为复杂的时空调度问题,一天有几千万乘客在不同的时空中发出需求,也有大几百万司机在不同的时空出现,每一次不同的派单都会影响不同的时空里供需分布,乘客和司机对派单响应是动态的,交通路况也不断地变化,优化目标也挺难刻画的,不光考虑全局的需求满足率,还得考虑人们心目中对服务的感觉等约束,把服务确定性描述清楚就不容易,是个开放的问题。若要跟围棋对比,我们简单抽象这个问题,一天完成2500万以上的订单,每2秒的一次撮合完成几百到上千的派单,一次撮合本身的计算复杂度非常高,可载客的车辆数和需求订单数远远大于派单数,组合的空间非常大10万以上,每2秒撮合都会影响到未来的时空上供需分布,就像下棋每一步落子都会影响棋局变化,一天共撮合43200次,时空的变化是(10万)43200次方的量级。滴滴也用强化学习算法来解这个问题,不断迭代和改进。
围棋的规则是确定的,是完美信息博弈,AlphaZero可以自己根据规则创造出棋谱,AlphaGo和AlphaZero在围棋上可以超过人类棋手。而在开放问题上,AlphaGo和AlphaZero目前还不能超越人类,例如,在星际争霸上还打不过人类,在王者荣耀上也胜不过人类。相信在大家共同努力下,技术不断突破边界,我们人类也有信心驾驭它,为人类的智慧不断增长而服务。在不同的战场,我们一起加油。
再次引发争议:
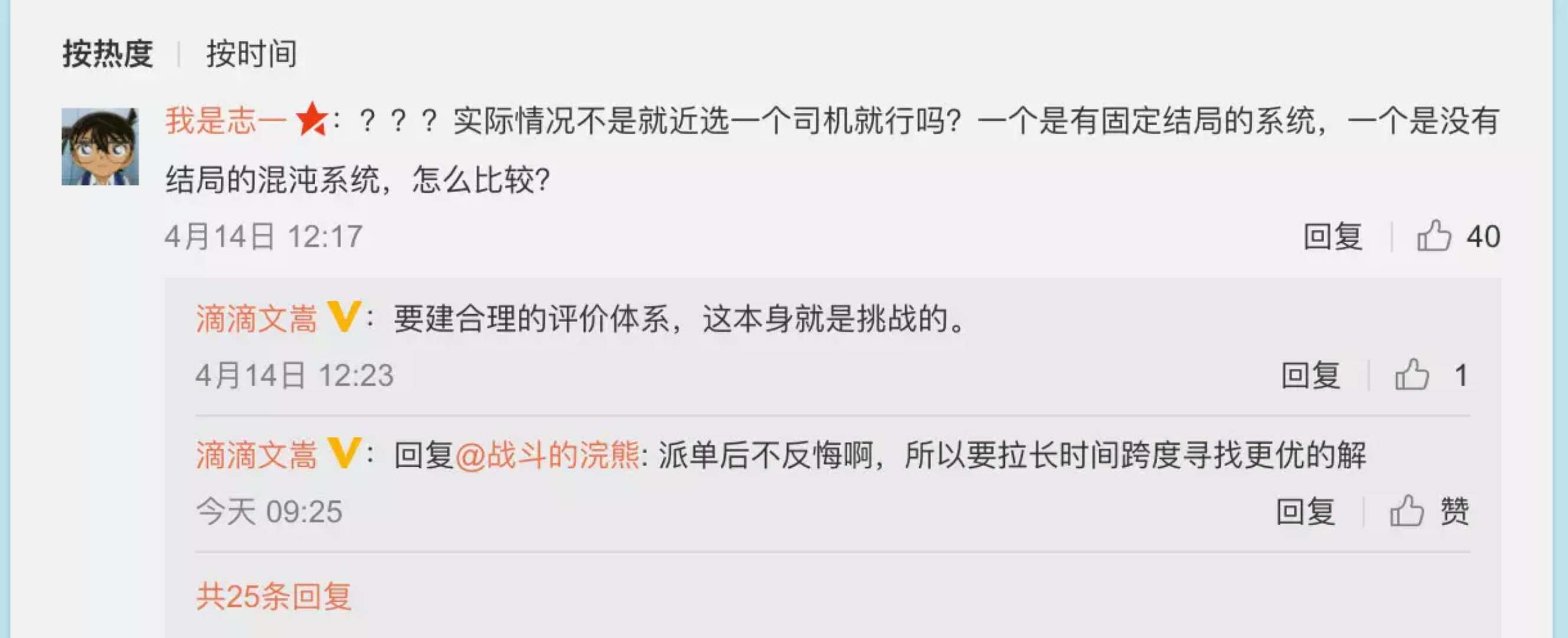
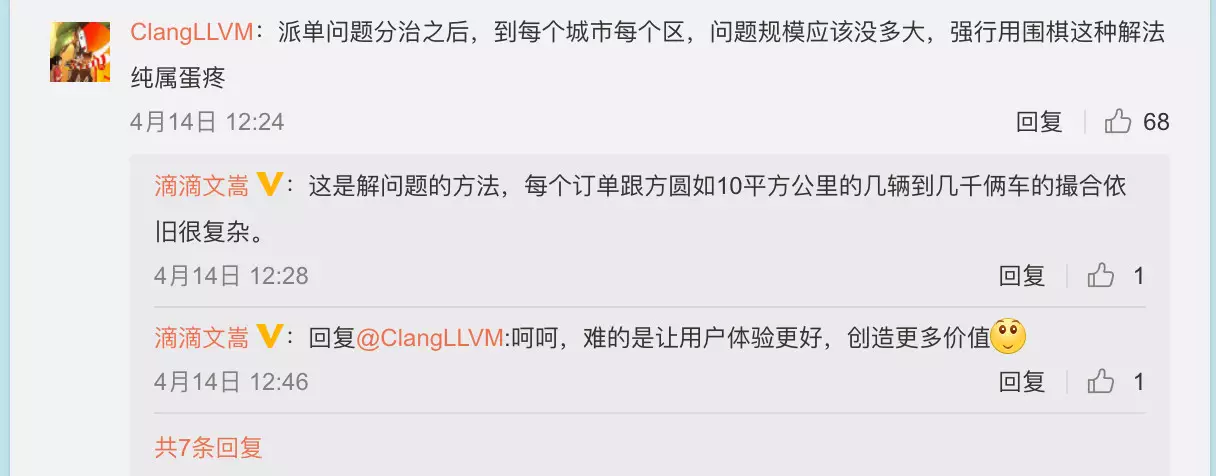
章文嵩对围棋最多361步这个说法进行更正和对分区来处理的工程解法进行解释。
章文嵩:围棋最多361步这个说法不准确,抱歉!没有考虑到打劫和提子的情况,感谢大家的讨论提升了我的认知。围棋的复杂度不是无限提升的,不能反复打劫,提子后空间也有限,聂棋圣在微博上说有专家团队研究过围棋变化是10的808次方。还是挺想学习一下里面的计算方法。
 章文嵩:大家提到了分区来处理的工程解法,如以2公里为半径画一个圆,面积约12平方公里,里面有非常多订单需求和可用司机需要计算相关性。工程上实际处理的复杂度已经很高,约1年前滴滴对外公布的路径规划量是200亿次一天,大部分是分单系统调用的,平摊到每一秒约23万次,高峰时一秒钟处理1百万次路径规划。
章文嵩:大家提到了分区来处理的工程解法,如以2公里为半径画一个圆,面积约12平方公里,里面有非常多订单需求和可用司机需要计算相关性。工程上实际处理的复杂度已经很高,约1年前滴滴对外公布的路径规划量是200亿次一天,大部分是分单系统调用的,平摊到每一秒约23万次,高峰时一秒钟处理1百万次路径规划。
来自:云头条